こんにちは！
データサイエンティストのウマたん(@statistics1012)です！
今回は中心極限定理について解説していきます！中心極限定理とは「サンプルサイズnが大きくなることで、母集団がどのような分布であっても標本平均の分布は平均\(μ\)、分散\(\frac{σ^{2}}{n}\)の正規分布に近似する定理」と考えられています！
この記事では、中心極限定理の定義について解説しつつ、サイコロの例をつかって正規分布に近似していく様子を見ていきます！
・中心極限定理の定義について解説！
・中心極限定理の挙動をPythonで見てみよう
以下のYoutube動画でも解説しているのであわせて是非チェックしてみてください！
中心極限定理について解説！
中心極限定理とは「サンプルサイズnが大きくなることで、母集団がどのような分布であっても標本平均の分布は平均\(μ\)、分散\(\frac{σ^{2}}{n}\)の正規分布に近似する定理」です。
いきなり正規分布という単語が出てきたため混乱すると思うので、今回はサイコロの例を使って、中心極限定理を見ていきましょう！
まず前提として母集団から\(n\)個の標本\(X_{n}\)を無作為抽出した場合、その平均は以下の式で表すことができます！
\(\bar{X} = \frac{\sum_{i=1}^{n} X_{i}}{n}\)
これを中心極限定理で考えてみると、「\(\bar{X}\)の分布はサンプルサイズ\(n\)を増やすことで、正規分布に近似される」ことが言えるはずです！
そして今回はサイコロの例を使って見ると、「サイコロの目の平均のサンプルサイズを増やすことで、正規分布に近似される」と言い換えることができます！
サイコロを100回振った時のサイコロの出目の平均値を計算するという施行を何回も繰り返すと、その平均値の分布は正規分布に近づくということなんです！
実際に中心極限定理の挙動を見てみよう！
実際にPythonでサイコロを100回振った場合のサイコロの目の平均のヒストグラムを見て、正規分布に近づいているか確認してみましょう！そして標本平均を5回、10回、100回、10000回と抽出してみましょう。
Pythonのコードは以下の通り！サイコロの目はnumpy.randomのrandint関数で生成して、その平均を出力してみましょう！その後、matplotlib.pyplotやseabornを使ってヒストグラムを出力してみることを試みてみましょう！
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
total = []
fig, axes = plt.subplots(1,4,figsize=(10,5))
for j,n in enumerate([5,10,100,10000]):
for i in range(n):
X_n = np.random.randint(1,6,100)
X_mean = np.mean(X_n)
total.append(X_mean)
sns.distplot(total,kde=True,ax=axes[j],label="n={}".format(n))
axes[j].legend()
total = []
plt.show()
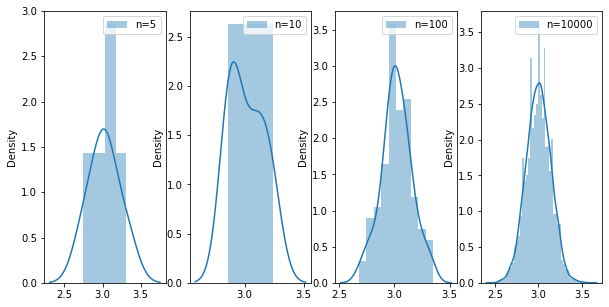
\(n\)=5, 10とした場合でも、正規分布にかなり近いことが分かりますね。そして\(n\)=10000ならほぼ正規分布といっても過言ではないでしょう！試行回数を増やせば増やすほど、分布の形が分かりやすくなりますね！
中心極限定理 まとめ
本記事では中心極限定理についてまとめました！中心極限定理のベースとなる大数の法則についてもあわせてチェックしてみてください。
また、中心極限定理を用いる代表的な分布として二項分布が挙げられます！スタビジでは二項分布の解説と正規分布への近似まで解説しているので、是非見てください！
このようなデータサイエンスの力を身に付けるためにはスタビジの記事やスクールを活用すると良いでしょう。
そして僕の経験を詰め込んだデータサイエンス特化のスクール「スタアカ（スタビジアカデミー）」を運営していますので，興味のある方はぜひチェックしてみてください！
AIデータサイエンス特化スクール「スタアカ」
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」！！
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています！
Pythonが初めての人でも学べるようなカリキュラムしておりますので是非チェックしてみてください！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
データサイエンスに関する記事はこちら！
データサイエンスを勉強できるスクールやサイトは、ぜひこちらを参考にしてみてください！
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
