こんにちは!
データサイエンティストのウマたん(@statistics1012)です。
有名な機械学習手法の一つに決定木があります!非常に良く使われる王道な手法です。
今回はそんな決定木について見ていきましょう~!
それでは、決定木について徹底的に見ていきましょう!
決定木の概要を掴んだあと、RとPythonで実装してみて最終的に決定木を使った応用手法も取り上げていきますよ!
Youtubeでも解説しているので、ぜひこちらもチェックしてみてください!
目次
決定木とは
比較的新しい文献から決定木に関する記述を引用してみましょう!
2009年の論文です。
CART is a rule-based method that generates a binary tree through binary recursive partitioning that splits a subset (called a leaf) of the data set into two subsets (called sub-leaves) according to the minimization of a heterogeneity criterion computed on the resulting sub-leaves. Each split is based on a single variable; some variables may be used several times while others may not be used at all.
引用元:Google-“CART algorithm for spatial data: Application to environmental and ecological data”
決定木の分類アルゴリズムの1つであるCARTの説明について述べてあります。
詳しく知りたい方は論文を見てみてください。
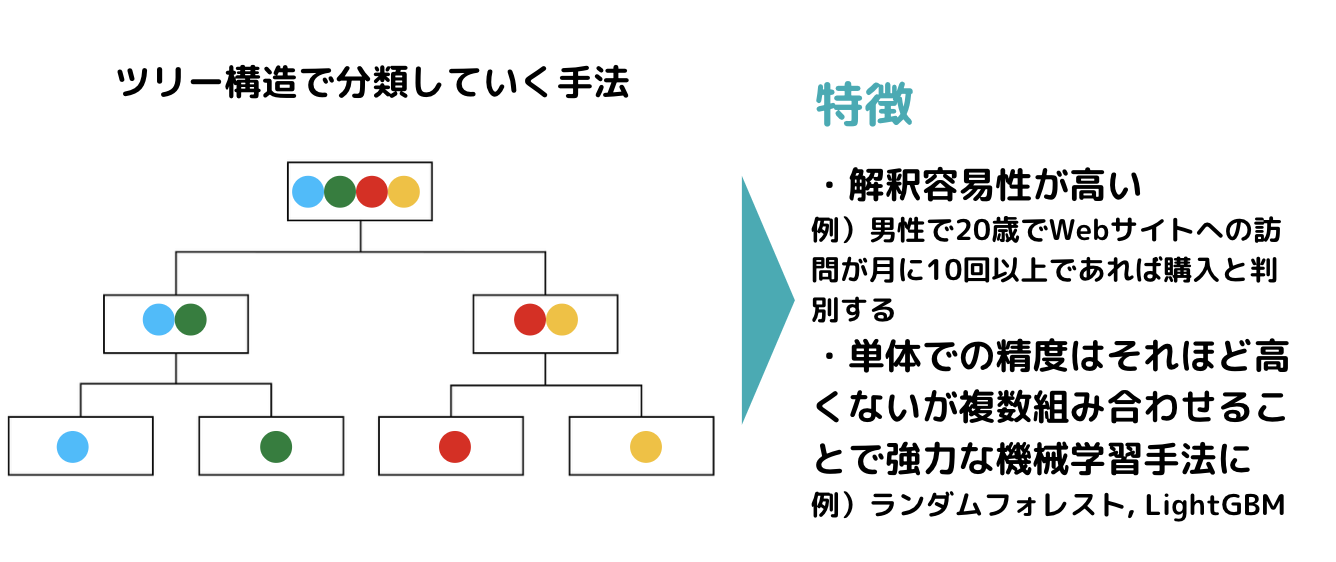
決定木っていうのはその名の通り木構造でデータ分類していく手法で、そこそこの精度と結果の視認性から実務の場で良く用いられています!
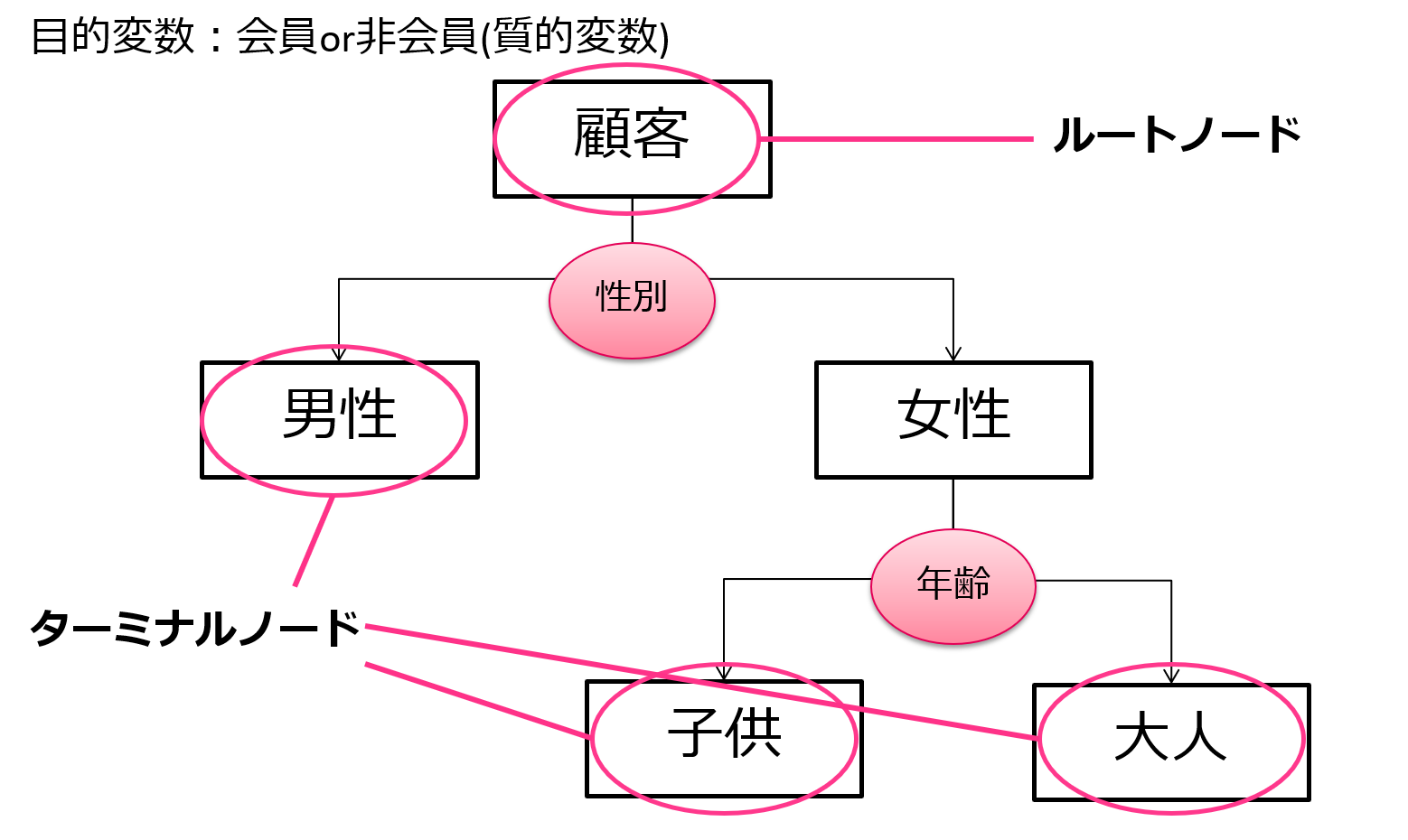
非常に簡易的な例ですが、会員か非会員かどうかを多くの変数で判断するような判別を行うとします。
その時、まずは性別による影響が強いようなので性別で分類、続いて年齢による影響が強いようなので年齢で分類・・・
このように木構造が下に伸びていって分類することができます。
分類された箱をノードと呼びます。
そしてもうこれ以上分類されない最後のノードをターミナルノードと呼びます。
この図の例だと、男性・子供・大人がターミナルノードですね。
もっと一般的な例で考えてみましょう!
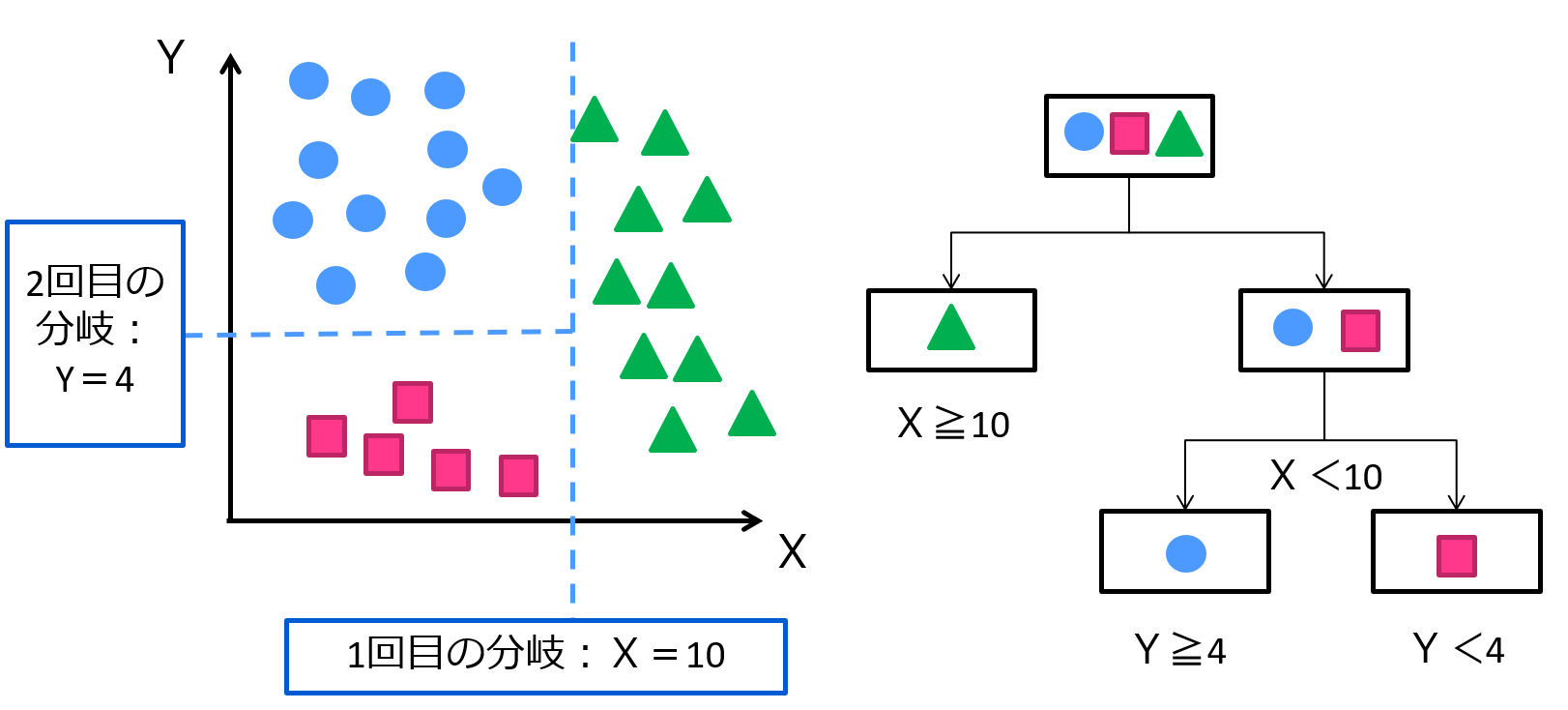
こんな感じ!この例は3つのカテゴリー質的変数をX,Yの説明変数を用いて上手く分類している例です!
こんな感じで分類したあとに視覚的にどんな変数が一番分類に効いているのかなどが分かりやすいのが特徴です!
その他の手法含む機械学習系、その他のAI用語を一挙にまとめた以下の記事も合わせて要チェックです!

決定木のアルゴリズム(CART)
それでは、そんな決定木のアルゴリズムを見ていきましょう!
決定木のアルゴリズムはいくつかあるんですが、最も有名なのがCART!
先ほどの論文でもCARTが用いられていましたね。
CARTは決定木の数あるアルゴリズムの中でも最も良く使われる手法であり、L.Breimanらによって1970年代初めごろから研究が始められ、1980年代の前半に公開されたアルゴリズムです。
元田先生らが書いたデータマイニングの基礎を参考にしてみていきましょう!
CARTは目的変数を最も効果的に分類できるように、 Gini係数という指標を用いて分岐を行います。
Gini係数はクラスの偏り具合を表す指標であり、不純度と表現されます。
特定のクラスのデータばかりであるほど0に近く、どのクラスも均等に存在する場合に大きな値を取る性質を持ちます。
Gini係数は以下の式で表され、この値は小さければ小さいほど良いということが分かっています。
\(GINI(t)=1-\displaystyle \sum_{ j = 1 }^{ k } p^2{(j|t)}\)
この時、\(p{(j|t)}\)はノードt内のクラスjの割合を示します。
(引用元:データマイニングの基礎 (IT Text))
Gini係数を計算後、親ノードと子ノードのGini係数の差が大きいものを分岐の条件として選びます。
そして分割できなくなるまで続けていき、最終的にそれぞれのデータが属するノードのことをターミナルノードと呼びます。
Rを使って決定木を実装してみよう!

それでは、最後に決定木を用いた分析を行ってみましょう!
データはなんでも良いんですが、簡易的にRにデフォルトで入っているirisデータを使いましょう!
あやめの種類を分類したデータで目的変数は3カテゴリーの質的変数、説明変数は花びらの幅とか4つです。
サンプルは150個で、分類しやすいデータなのでどんな手法でも割と簡単に分類できるんですが、どうなるでしょう!
今回は決定木以外にランダムフォレストとSVMとニューラルネットワークで比較しました。
ちなみにランダムフォレストは決定木とアンサンブル学習を組み合わせた協力な機械学習手法。
ランダムフォレスト
pred.forest setosa versicolor virginica
## setosa 29 0 0
## versicolor 0 25 1
## virginica 0 2 18
決定木
pred.cart setosa versicolor virginica
## setosa 29 0 0
## versicolor 0 26 3
## virginica 0 1 16
SVM
pred.svm setosa versicolor virginica
## setosa 29 0 0
## versicolor 0 25 1
## virginica 0 2 18
ニューラルネット
pred.nn setosa versicolor virginica
## setosa 29 0 0
## versicolor 0 25 2
## virginica 0 2 17結果はこんな感じになりました!
どれもいい感じに分類できてますね~!
本来は何回かシミュレーションやって誤判別率の平均取った方がいいんですが、今回は簡易的に行いました!
Pythonを使って決定木を実装してみよう!

続いて決定木についてPythonを使って分類していきましょう!
Pythonでもirisデータを使用していきます。
Rの場合はirisデータにそのままデータセットがデータフレーム型で入っていましたが、Pythonの場合は説明変数データとそれに紐づくラベルデータ、変数名などがリストで入っていることに注意しましょう!
そのためirisからデータを取り出す作業をしています。
# 特徴量とターゲットの取得
data = iris['data']
target = iris['target']
決定木を使った応用手法

さて、最後にそんな決定木を応用した手法群について見ていきましょう!
決定木単体ではそれほど高い精度は見込めないのですが、アンサンブル学習という方法と組みわせることで最強の精度を叩きだす手法になります。
アンサンブル学習とは簡単に言うと、複数モデルを作って色んな方法で組み合わせる手法です。

ここでは、そんな「決定木×アンサンブル学習」としてランダムフォレストとXgboostとLightGBMについて解説していきます。
ランダムフォレスト
ランダムフォレストでは、決定木を複数個作ってそれらの多数決で最終的な結果を決めます。
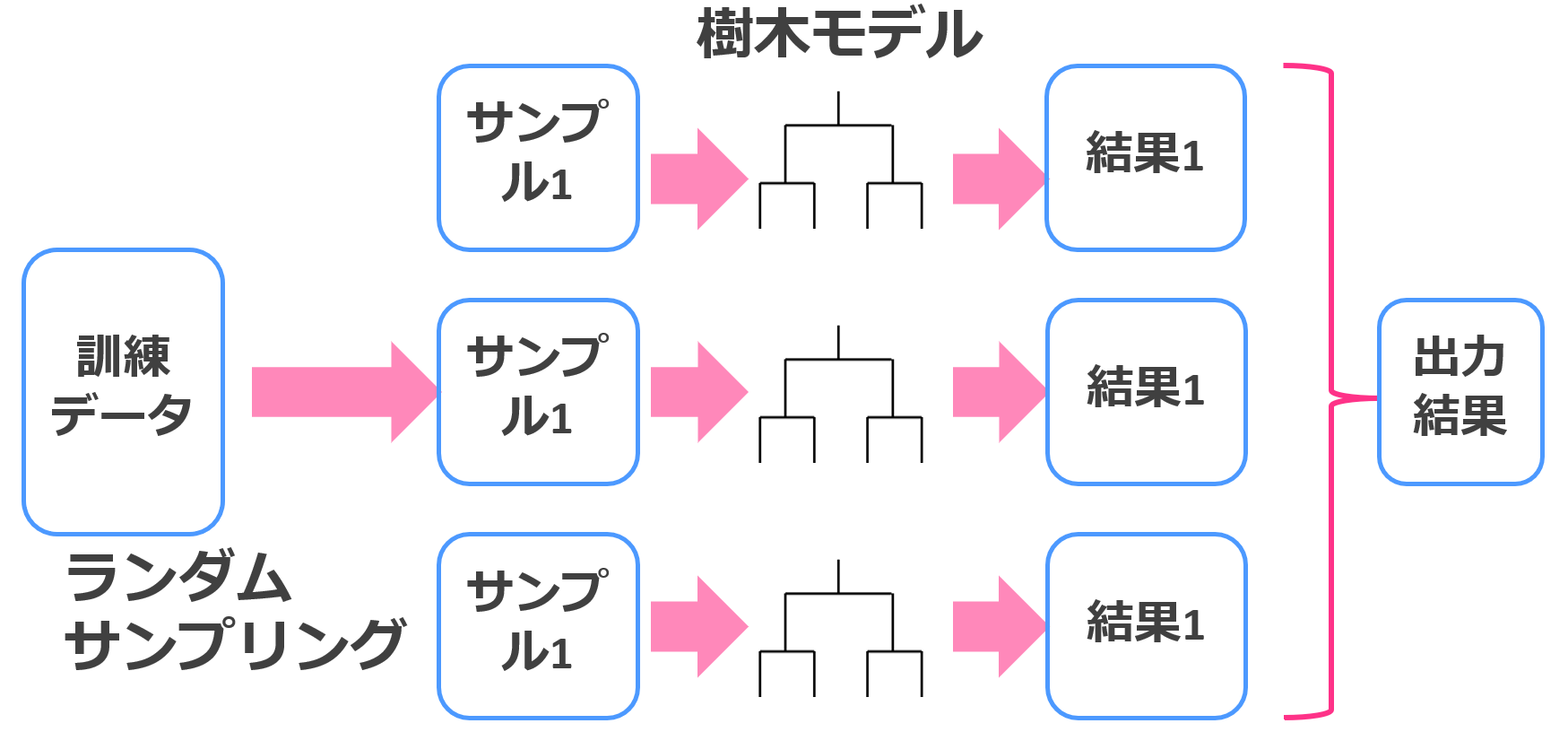
この方法はアンサンブル学習の中でもバギングと呼ばれます。
分類の時は多数決ですし、回帰の時は平均を取ります。
通常の決定木よりも大幅な精度向上が見込めるんです。
詳しくは以下の記事でまとめています!

XGBoost
続いてはXgboost。
Xgboostでもランダムフォレストと同様に複数の決定木を生成し学習していくのですが、若干学習方法が違います。
ランダムフォレストは並列に複数個の決定木を生成して多数決を取るタイプでしたが、
Xgboostは直列に複数の決定木を生成して精度を改善していくタイプ。
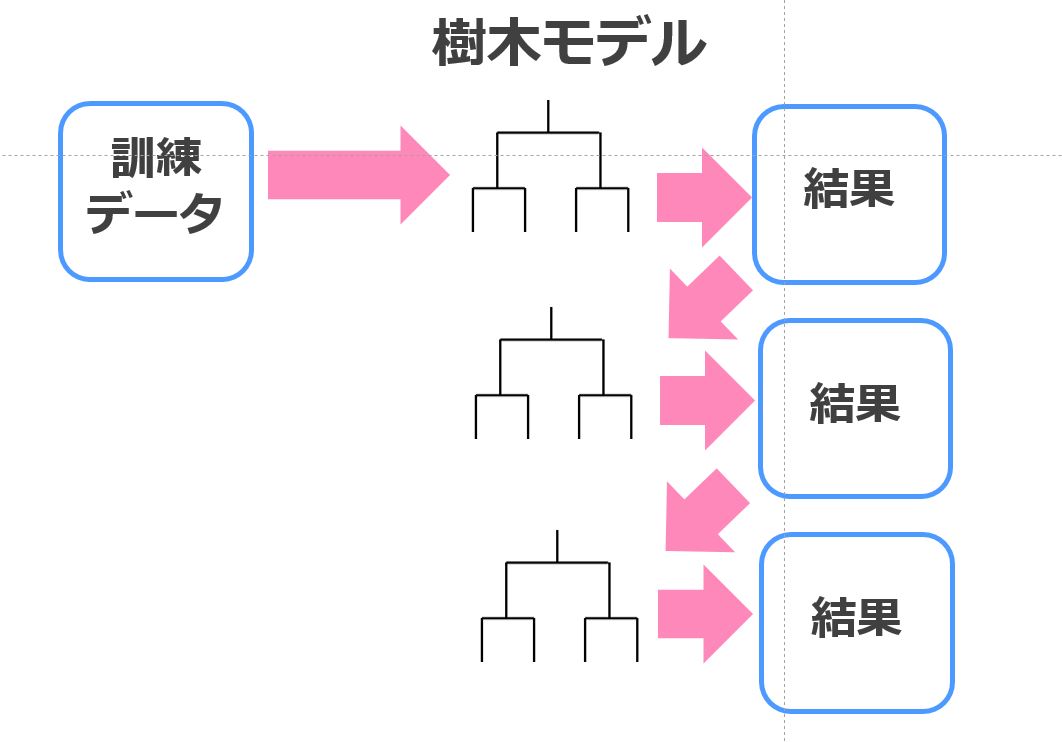
前の決定木では上手く判別できなかった部分に焦点を当てて次の決定木で学習していくイメージです。
単体だと上手く判別できない要素も複数の決定木を直列に組み合わせることで判別できるようになるんですよねー!
ランダムフォレストはバギングと呼ばれるアンサンブル学習を使っていましたが、Xgboostではブースティングと呼ばれるアンサンブル学習を使っています。
ちなみにXgboostの方が高い精度が見込めるので、特に何も考えずXgboostを使うことが多いです。
XGBoostについては以下の記事でまとめています!

LightGBM
XGBoostを改良した最強の手法がこちらのLightGBM!
LightGBMは決定木の学習方法がXGBoostと若干違い、効率よく学習していくことが可能なんです。
そのため学習スピードが圧倒的に速く、Mnistのデータを分類した場合約10倍ほどの差が生まれました。
以下の記事でLightGBMについて詳しくまとめています!
決定木の勉強法
そんな決定木をより深く、そしてさらなる機械学習手法の架け橋となるための勉強方法についてまとめていきます!
書籍で理論を勉強する
決定木に関しては以下の書籍を読むといい感じに載っていますので読んでみると良いでしょう!
決定木は機械学習手法の基本のキです。
決定木から他の機械学習手法まで広範に押さえています。
Webサイトで実装を勉強する
理論は書籍で勉強するほうがオススメですが、実際のデータを加工して決定木を実装していく過程を学ぶなら以下のUdemyの講座を受講してみてください!
【初学者向け】データ分析コンペで楽しみながら学べるPython×データ分析講座
| 【オススメ度】 | |
|---|---|
| 【講師】 | 僕自身!今なら購入時に「XTWY2UJ4R5F3」という講師クーポンコードを入れると90%オフ以上の割引価格になりますのでぜひご受講ください! |
| 【時間】 | 4時間 |
| 【レベル】 | 初級~中級 |
このコースは、なかなか勉強する時間がないという方に向けてコンパクトに分かりやすく必要最低限の時間で重要なエッセンスを学び取れるように作成しています。
アニメーションを使った概要編とハンズオン形式で進む実践編に分かれており、概要編では体系的にデータ分析・機械学習導入をまとめています。
データサイエンスの基礎について基本のキから学びつつ、なるべく堅苦しい説明は抜きにしてイメージを掴んでいきます。
統計学・機械学習の基本的な内容を学び各手法の詳細についてもなるべく概念的に分かりやすく理解できるように学んでいきます。
そしてデータ分析の流れについては実務に即したCRISP-DMというフレームワークに沿って体系的に学んでいきます!
データ分析というと機械学習でモデル構築する部分にスポットがあたりがちですが、それ以外の工程についてもしっかりおさえておきましょう!
決定木だけでなく様々な機械学習の実装方法やデータコンペティションでの実践分析方法が学べます!
是非興味のある方は受講してみてください!
また、さらに踏み込んでデータサイエンスについて学びたいのであれば、当メディアが運営する「スタアカ(スタビジアカデミー)」がオススメ!
 公式サイト:https://toukei-lab.com/achademy/
公式サイト:https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン:1280円/月 プレミアムプラン:149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
データサイエンティストとしての自分の経験をふまえてエッセンスを詰め込んだのがこちらのスタビジアカデミー、略して「スタアカ」!!
当メディアが運営するスクールです。
24時間以内の質問対応と現役データサイエンティストによる複数回のメンタリングを実施します!
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください!
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています!
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます!
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
決定木 まとめ
決定木は簡単に実装できて、かつ結果も分かりやすい優秀な手法です。
是非使ってみてください!
決定木は機械学習の序章にすぎません。
機械学習の世界は決定木をはじまりに大きく広がります。
機械学習手法に関して深く勉強したい方は以下の記事を参考にしてみてください!

また、機械学習を実装する上で切っても切れない関係であるPythonに関しては以下の記事でまとめています!