こんにちは！
デジタルマーケターやらデータサイエンティストみたいなことを事業会社でやったのち、独立して事業展開しているウマたん（@statistics1012）です！
いかに自社の事業にAIを絡ませていくかみたいな話を仕事でよくしています。
AI(人工知能)や機械学習というと何でも出来そうなイメージがありますが、それはまやかし。
「AIだったらなんでも出来るんだろっ！」という老害おじさんがよく出現します。
ただ、AIや機械学習をちゃんと理解するには難しい数学が必要な気がするという人も多いのではないでしょうか？
もちろん複雑な数学が必要な場面もありますが、基本は高校で習うカンタンな微積と行列が分かっていれば大丈夫です！
ちなみに実装だけなら数学なんていりません。
ただやはりブラックボックスになりがちなAIの中身を理解していく上では数学は必要。
この記事では、まずそもそもAIとはどのような範囲を指すのか定義を定めた上でそれらのAIや機械学習を学習するために必要な数学基礎固め方法についてまとめていきます！
以下のYoutube動画でもまとめているので動画で見たい！という方はこちらもあわせてチェックしてみてください！
目次
そもそもAI(人工知能)とは？機械学習との違いは？
様々な場で使われているAIという言葉ですが、実際にどのような定義で使われているのかご存知でしょうか？
まずは、数学の話に入る前にAIそのものの概念的な理解が必要です。
AI(人工知能)と聞くとディープラーニングを思い浮かべる人も多いのではないでしょうか？
しかしディープラーニングが登場したのは2006年であり、人工知能という言葉はそれよりもずっと前からある言葉。
必ずしもAI(人工知能)＝ディープラーニングとは言えないのです。
よく言われるのが、AI(人工知能)の中に機械学習がありその中にディープラーニングがあるという構造。
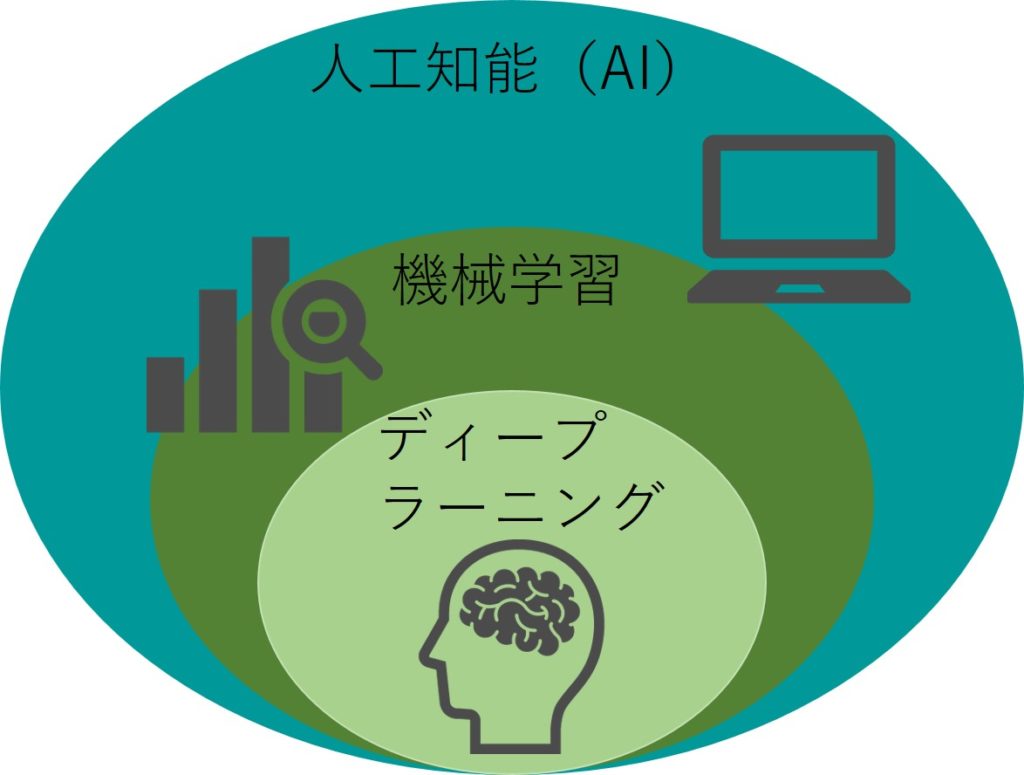
AI(人工知能)という言葉自体は1950年代からあるんです。
AIには実は第1次～第3次ブームがあり、現在はその第3次ブームであると言われています。
第1次ブームではルールベースのアルゴリズム、第2次ブームではニューラルネットワーク、第3次ではニューラルネットワークを深層化したディープラーニングが中心になっています。
このようにAIは人によって捉え方が違うため、軽々しく使ってはいけないのです。
AIに関してもっと詳しく以下の記事でまとめています！
AI・機械学習に必要な数学の分野
それではAIがそもそも何なのか理解できたところで、そんなAI学習に必要な数学のレベルについてまとめていきましょう！
AIに必要な数学の分野は大きく分けて3つあります。
・微分積分
・線形代数
・確率統計
微分積分の知識
微積分というとどのようなイメージを持つでしょうか？
高校数学で習った微分を思い出してみてください。
なんとなーく、微分は傾きを求めるものというイメージがありますでしょうか？？
そう、カンタンに言ってしまうと微分とはある関数の接線の傾きを求める作業なんです。
では、接線の傾きを求めることができると何が嬉しいのでしょう？
実は、傾きが0になるところを求めることできるとすっごい嬉しいんです。
AIの学習には色んなデータを使います。
そして、色んなデータを元にモデルを作って元データへフィッティングしたり未知のデータを予測したりします。
その値が果たして妥当なのか全然ダメなのかは正しい値と推定した値の差（誤差）の総量で求めます。
その総量をAIの分野では損失関数と言いますが、損失関数をなるーーべく小さくすると良いモデルになります。
例えば、損失関数が(y= x^2)だったとしましょう。
(y= x^2)が一番小さい部分を求めるにはどうしたらよいでしょう？
(y= x^2)を微分すると、(y= 2x)になります。
傾きが0になる位置は・・・・ここ！
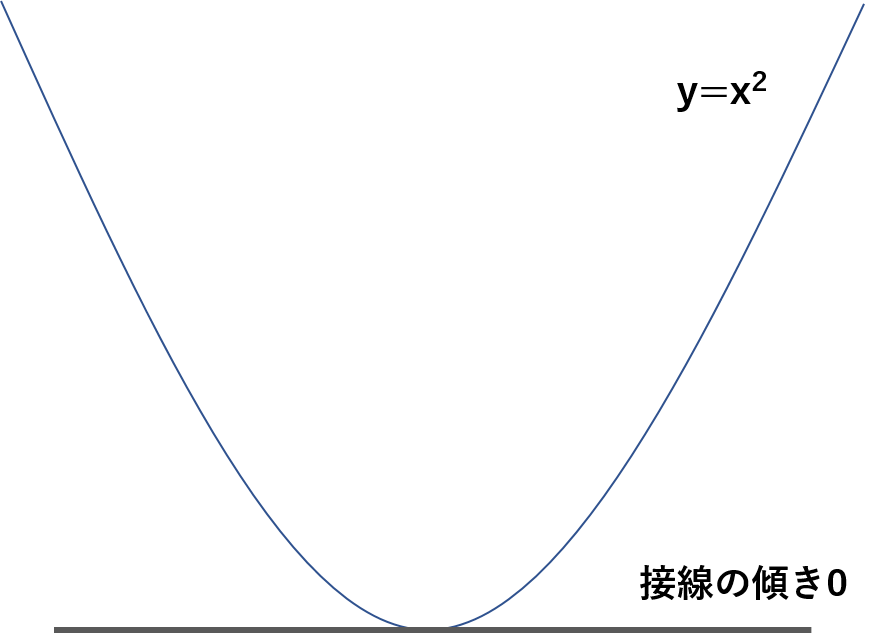
接線の傾きが0の点を求めることで、二次関数の最小値を求めることができましたね！
損失関数が最小になるということは推定値と実測値の誤差が少ない良いモデルを構築できたということになります。
実際のケースはこんなに単純ではありませんが、変数が増えても微分して損失関数の最適解を求めるという考え方は同様です。
線形代数の知識
続いて、線形代数！
線形代数って、正直高校や大学の時はムダな知識だなーと思っていた時期がありました。
しかーし、線形代数は大量のデータを扱うAIの分野で非常に重要な知識なんです！
線形代数がAIを学ぶ上で一番重要な基礎知識だと言っても過言ではないです。
線形代数とは、カンタンに言うと「たくさんあるデータをまとめて計算するマジック」
たくさんの変数とデータを用いる重回帰分析という手法があります。
重回帰分析の例を見ながら線形代数がどのようなものかカンタンに学んでいきましょう。
n個のサンプルがあるデータセットで一つの目的変数をp個の説明変数で説明するモデルを作ると以下のようになります。
$$y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}+\epsilon_i, \epsilon_i \sim N(0,\sigma^2),(i=1,\cdots,n)$$
\(y\)：目的変数、\(\beta_0\)：ある定数、\(\beta_j\)：ある係数、\(\epsilon\)：誤差項を表しています。また添え字のiはサンプルを表します。
\(\beta_0\)や\(\beta_j\)が推定したい値。
\(x_{ip}\)が実際のデータが入る部分。
この式を基に、推定値と実際の値の誤差の2乗和を損失関数として定義し偏微分で各パラメータ\(\beta_0\)や\(\beta_j\)を求めていきます。
ここでは、そんなものなのかーと思っておいて欲しいのですがこの作業を線形代数を使って表すと非常にコンパクトになります。
まずは、先ほどの長ったらしい式は行列でコンパクトに表すことができます。
\begin{eqnarray*}
{\bf y}&=&{\bf X}{\bf \beta}+{\bf \epsilon},{\bf \epsilon} \sim N({\bf 0},\sigma^2{\bf I_n})\\
\end{eqnarray*}
\({\bf y}\):n次元ベクトル、\({\bf X}\):n×(p+1)の行列ただし一列目は1を並べた列、\({\bf \beta}\):(p+1)次元ベクトル、\({\bf \epsilon}\):n次元ベクトル。
そして\({\bf \beta}\)は以下のように推定されます。
\begin{eqnarray*}
\hat{{\bf \beta}}&=&{({\bf X}^{T}{\bf X})}^{-1}{\bf X}^{T}{\bf y}\\
\end{eqnarray*}
従って、\({\bf y}\)の推定値\(\hat{{\bf y}}\)は次のようになります。
\begin{eqnarray*}
\hat{{\bf y}}&=&{\bf X}{({\bf X}^{T}{\bf X})}^{-1}{\bf X}^{T}{\bf y}\\
\end{eqnarray*}
まずは、こんなスッキリ表すことができるんだなーくらいでも大丈夫です。
ただ、このような数式展開はAIの分野だと普通であり、これは重回帰分析という基本のキなんです。
ほとんどのAI・機械学習関連の書籍が線形代数ベースで定式化されているため、線形代数が分からないと死んじゃいます。
少なくとも、線形代数の基礎的な部分は理解しておきましょう！
確率統計の知識
最後に確率統計の知識。
確率統計は微積や線形代数と比較すると苦手意識のない人が多いのではないでしょうか？
なぜなら確率統計は現実の世界に当てはめて理解することができるから。
平均や分散・標準偏差などの統計量なんてよーく目にしますし、
「この組み合わせって何通りあるっけ」
とか、
「これが出る確率は・・・？」
なんてことも実際にありますよねー！
それをもう少し拡張したのがAIにおける確率統計の世界なんです。
確率を語る上で非常に重要なのが確率分布。
サイコロは全ての値が等しく登場するので一様分布になりますが、実際のデータはそんなわけありません。
正規分布やカイ二乗分布、ポアソン分布など様々な分布を仮定することが多いです。
確率分布を広く理解することで、統計的検定やベイズ統計学の世界に足を踏み入れることができます。
AI・機械学習に必要な数学を基礎固めする方法
さてさて、AI学習に必要な数学について見てきましたが実際にこれらをどのように勉強していけば良いのでしょうか？
難書にぶつかってしまうと、一気にやる気がなくなってしまうので慎重に。
ここではなるべくカンタンに学べる方法についてまとめていきます。
最初にAIの全体感を掴む
いきなり理論に入るのではなく全体感を学ぶのがオススメです。
手前味噌ですが、僕自身が書いているこちらの書籍が取っ掛かりとしては良いかなと思います。
「俺たちひよっこデータサイエンティストが世界を変える」という書籍を出版しています。
あまり具体的なデータサイエンティストの仕事について分かりやすく書いている本が見当たらなかったので自分で執筆しました！
勾配ブースティング木のXGBoostを使ったビジネスシーンでの実装についてストーリー形式で簡単にまとめていますのでイメージをふくらませてもらうのにちょうど良いかと思います！
価格は300円ちょっとですし、Kindle unlimitedであれば無料で読めるのでぜひチェックしてみてくださいね！
続いてデータサイエンスや機械学習を網羅的に学んで感覚を掴むのであればAIデータサイエンス特化スクールの「スタアカ（スタビジアカデミー）」がオススメです！
公式サイト：https://toukei-lab.com/achademy/
| 【価格】 | ライトプラン：1280円/月 プレミアムプラン：149,800円 |
|---|---|
| 【オススメ度】 | |
| 【サポート体制】 | |
| 【受講形式】 | オンライン形式 |
| 【学習範囲】 | データサイエンスを網羅的に学ぶ 実践的なビジネスフレームワークを学ぶ SQLとPythonを組みあわせて実データを使った様々なワークを行う マーケティングの実行プラン策定 マーケティングとデータ分析の掛け合わせで集客マネタイズ |
24時間以内の質問対応と現役データサイエンティストによる1週間に1回のメンタリングを実施します！
カリキュラム自体は、他のスクールと比較して圧倒的に良い自信があるのでぜひ受講してみてください！
他のスクールのカリキュラムはPythonでの機械学習実装だけに焦点が当たっているものが多く、実務に即した内容になっていないものが多いです。
そんな課題感に対して、実務で使うことの多いSQLや機械学習のビジネス導入プロセスの理解などもあわせて学べるボリューム満点のコースになっています！
ウォルマートのデータを使って商品の予測分析をしたり、実務で使うことの多いGoogleプロダクトのBigQueryを使って投球分析をしたり、データサイエンティストに必要なビジネス・マーケティングの基礎を学んでマーケティングプランを作ってもらったり・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践してもらったりする盛りだくさんの内容になってます！
・BigQuery上でSQL、Google Colab上でPythonを使い野球の投球分析
・世界最大手小売企業のウォルマートの実データを用いた需要予測
・ビジネス・マーケティングの基礎を学んで実際の企業を題材にしたマーケティングプランの策定
・Webサイト構築してデータ基盤構築してWebマーケ×データ分析実践して稼ぐ
微分積分を学習する方法
微分積分の学習には以下のUdemy講座をオススメします。
教育サービスを提供するキカガクの代表取締役の方が丁寧に機械学習のアルゴリズムについて教えてくれます。
まあ機械学習の基本・土台となる単回帰分析を数式から学んでいくもの。
ビックリしたんですが、パワポではなく紙に手書きで進んでいくんです！
最初は抵抗があったものの、なるほど意外と分かりやすい。
よくよく考えたら学生時代の教育は先生が手書きで黒板に書いて進めてましたもんね。
書籍で学ぶより断然学びやすいです！
Udemyの講座は30日間返品無料なのでぜひ試してみてください！
微分はこのくらいのレベルで問題ありませんが、深く微分について学びたいなら以下の最適化数学の書籍が非常におすすめです！
ちょっと難しいですが、深くエッセンスの詰まった書籍。
数学側に主眼を置いていますが、AI/機械学習手法と絡ませながら学ぶとより一層学びが深まる良書です。
線形代数を学習する方法
線形代数を学ぶのにおすすめなのは先ほど紹介したUdemy講座の中級編！
本コースでは線形代数を学びながら重回帰分析まで展開していきます。
線形代数を学びながら微分も用いて定式化していきますよー！
実際に手計算で重回帰分析を行い、その後Pythonのscikit-learnを使って分析を行っていきます。
Pythonを使うとこんなにカンタンに計算できてしまうのかとビックリすると思いますが実際に手計算をする経験は有用。
数学の理解と一緒にPythonでの実装も学んでいくと理論と実務の両輪が上手くかみあってよいでしょう。
さらに線形代数を深く学びたい人はぜひ以下のUdemy講座をチェックしてみてください。
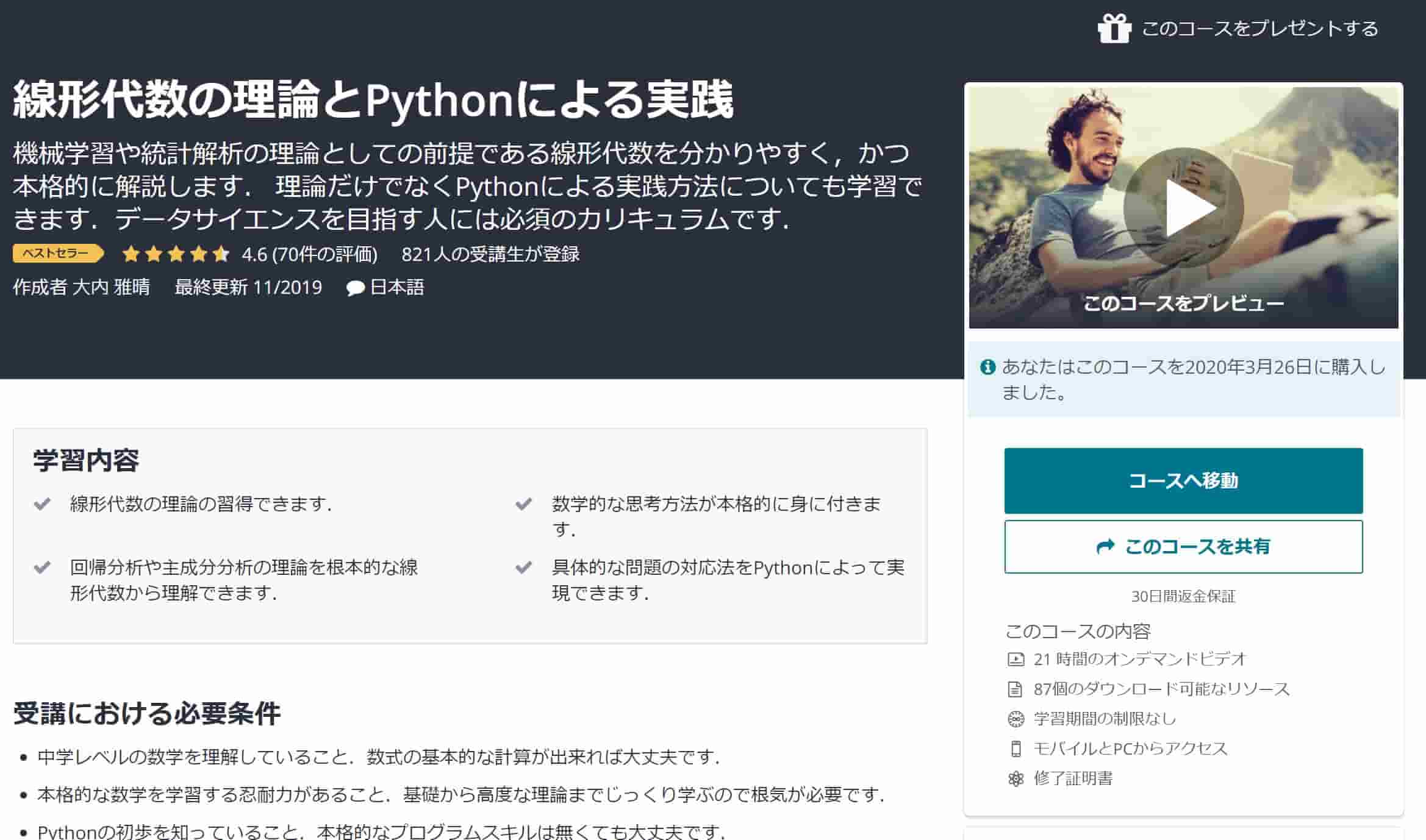
線形代数に特化した内容で初歩的な部分から応用まで幅広く網羅しています。
確率統計を学習する方法
確率統計に関してはUdemy講座だと以下の講座がおすすめです。
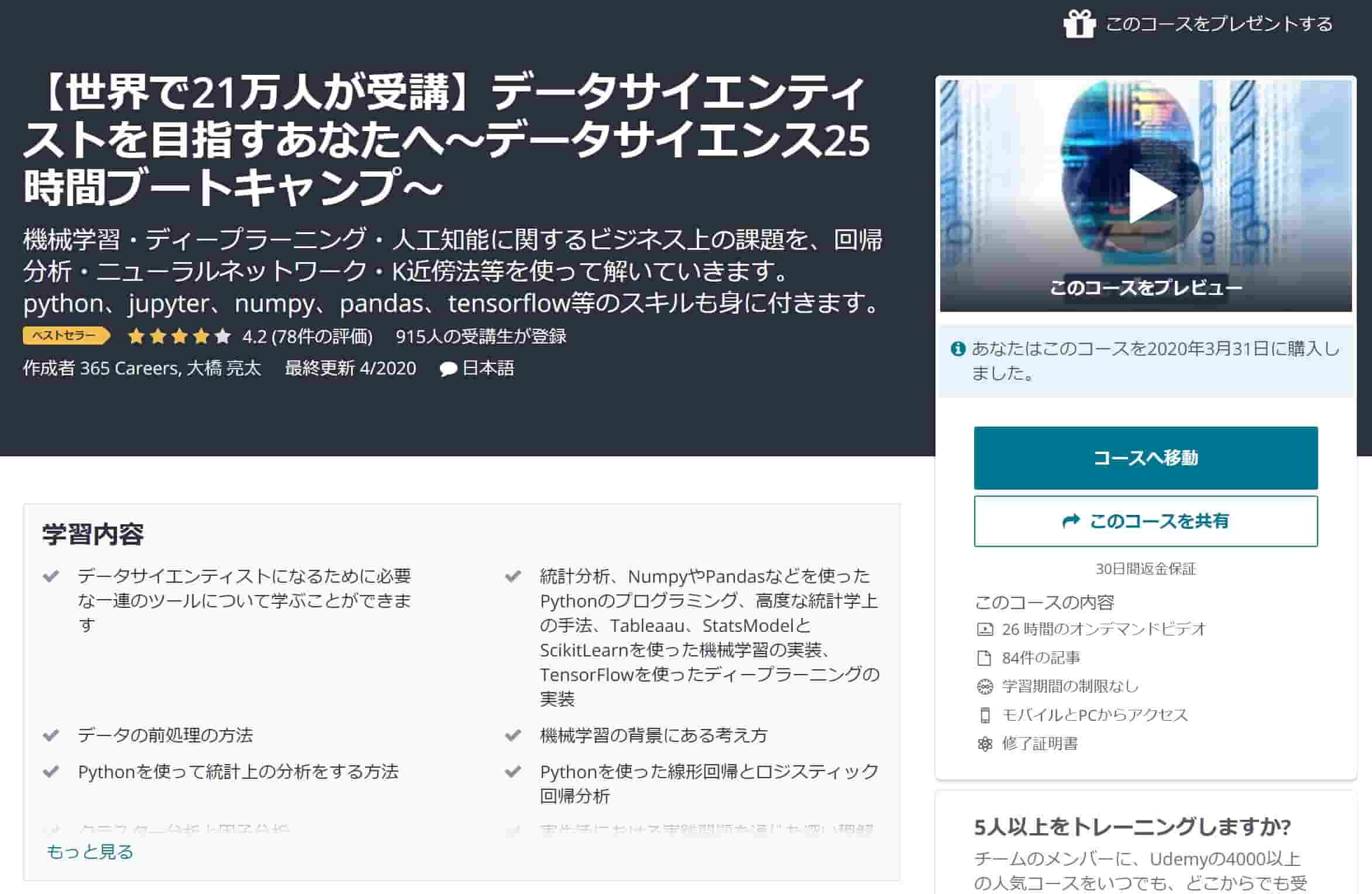
データサイエンスの分野を幅広くおさえている講座ですが、その中でも確率統計に関して初歩的な部分をしっかりおさえています。
コミカルな動画と共に学べるので非常に分かりやすいです。
ビジネスサイドに立ってどのようにデータを扱えばよいかという議論のもとデータサイエンスについて学べるので分かりやすくスーッと頭に入ってくると思います。
確率統計の本と言えるのか微妙で、もう既に数学の粋を超えて統計モデリングの世界に入ってきてしまっているのですが以下の書籍は本当におすすめ！
(2024/11/21 15:25:34時点 Amazon調べ-詳細)
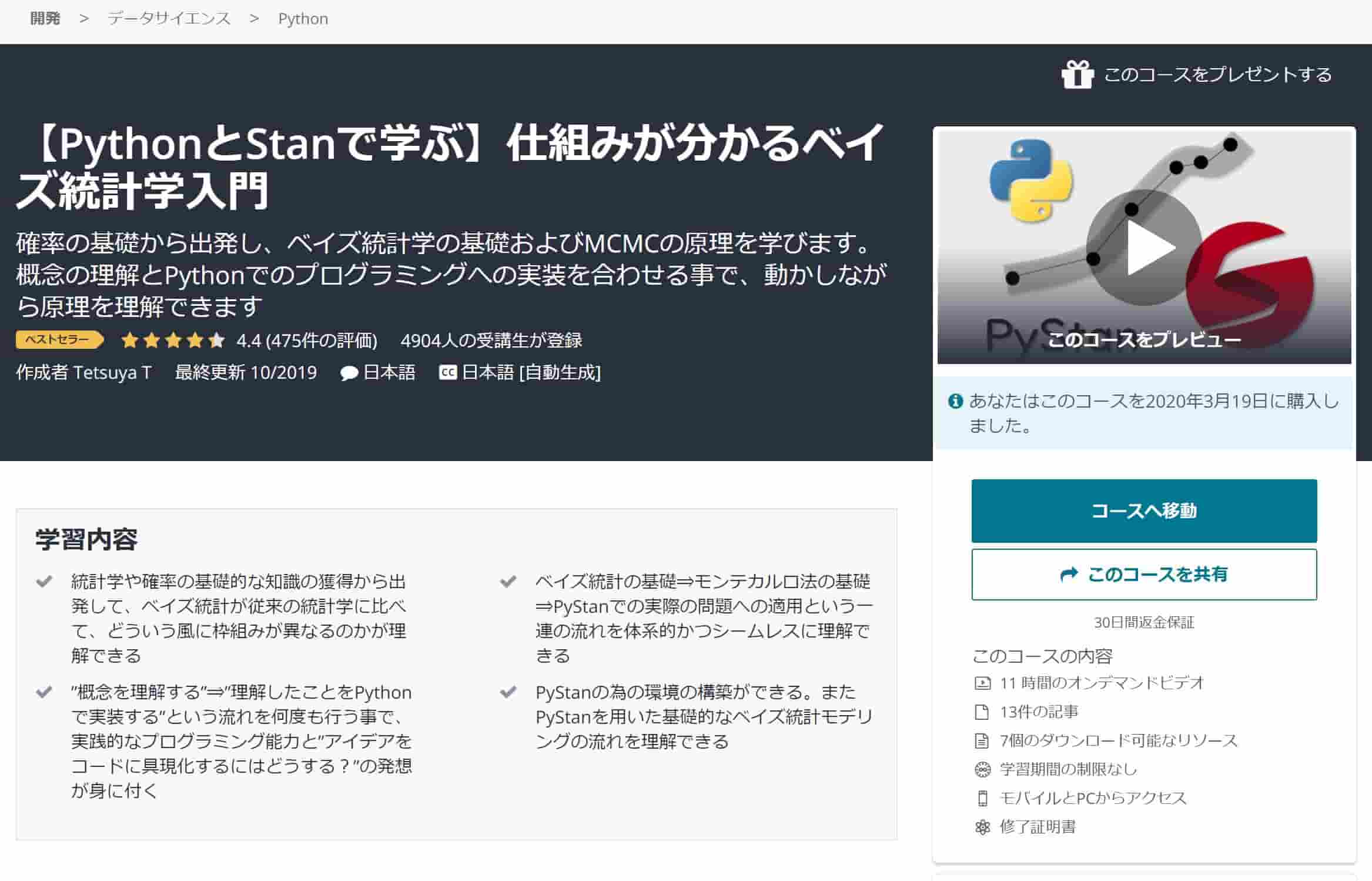
確率の話をさらに展開していくとベイズ統計学に行き着きます。
ベイズ統計学の世界に足を踏み入れたいなら以下のUdemy講座がおすすめ！
ベイズ統計学のおすすめ書籍は以下にまとめていますのでチェックしてみてください！
AI・機械学習の理解に必要な数学レベル まとめ
AI・機械学習を学ぶ上で
・数学のどんな分野を勉強すれば良いのか
・どのレベルまで持っていけばよいのか
・どのように勉強すればよいのか
についてまとめてきました。
数学だけ勉強していてもAI・機械学習・統計へどのように活かしていけばよいのかイメージがないとつまらないと思うので、なるべく実務と組み合わせた教材を選んで学ぶのがよいです。
この記事で紹介したUdemy講座・書籍は本当におすすめなのでぜひ試してみてください！
そして実際にある程度の数学の知識が入ってきたら本格的にAIを学ぶフェーズです。
AIを学ぶ書籍や講座について以下の記事でまとめていますのでぜひチェックしてみてください！
イラスト出典：Illustration by Stories by Freepik
スタビジのコンテンツをさらに深堀りしたコンテンツが動画と一緒に学べるスクールです。
プレミアムプランでは私がマンツーマンで伴走させていただきます！ご受講お待ちしております！
